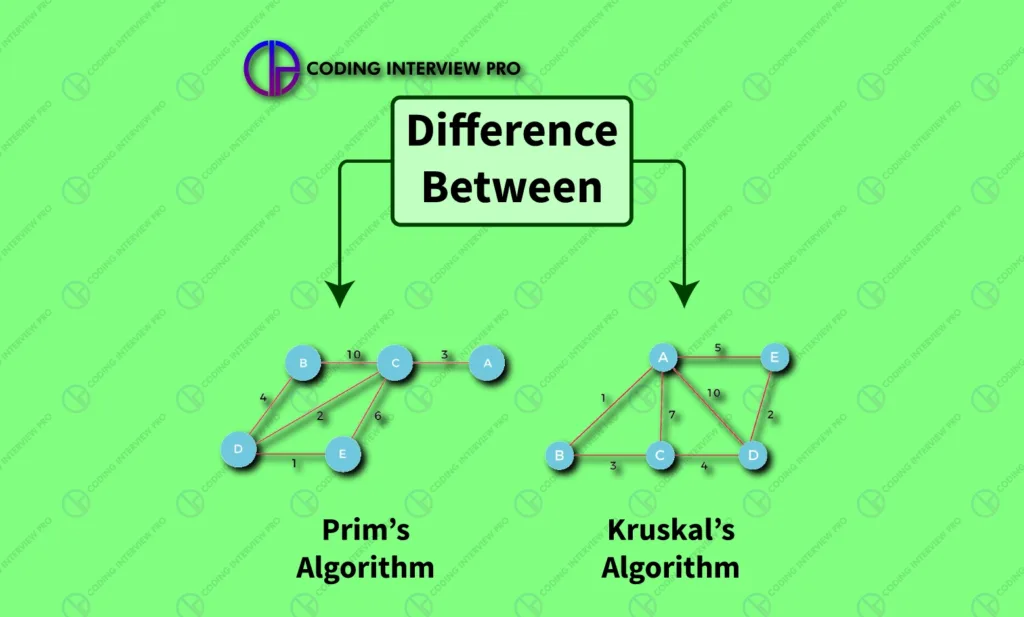
When it comes to finding the minimum weight spanning tree in a weighted graph, two common algorithms come to mind – Prim’s and Kruskal’s. These graph theory algorithms have significant applications in various fields, from network design to circuit optimization. While both algorithms share a common goal, they differ in their approach and efficiency. In this article, we’ll explore the Difference Between Prims and Kruskals Algorithm and similarities between Prims and Kruskals algorithms, analyze their time and space complexity, and highlight their respective advantages and disadvantages.
Table of Contents
- What is Prim’s Algorithm?
- What is Kruskal’s Algorithm?
- Differences between Prim’s and Kruskal’s Algorithm
- Differences between Prim’s and Kruskal’s Algorithm
- Time Complexity of Prim’s and Kruskal’s Algorithms
- Applications of Prim’s Algorithm
- Applications of Prim’s Algorithm
- Applications of Kruskal’s Algorithm
- Advantages of Prim’s Algorithm
- Advantages of Kruskal’s Algorithm
- Disadvantages of Prim’s Algorithm
- Dissadvantages of Kruskal’s Algorithm
- Conclusion
- FAQ
- Q: What is the difference between Prim’s and Kruskal’s Algorithm?
- Q: What is Prim’s Algorithm?
- Q: What is Kruskal’s Algorithm?
- Q: What are the similarities between Prim’s and Kruskal’s Algorithm?
- Q: What are the differences between Prim’s and Kruskal’s Algorithm?
- Q: What is the time complexity of Prim’s and Kruskal’s Algorithms?
- Q: What is the space complexity of Prim’s and Kruskal’s Algorithms?
- Q: What are the applications of Prim’s Algorithm?
- Q: What are the applications of Kruskal’s Algorithm?
- Q: What are the advantages of Prim’s Algorithm?
- Q: What are the advantages of Kruskal’s Algorithm?
- Q: What are the disadvantages of Prim’s Algorithm?
- Q: What are the disadvantages of Kruskal’s Algorithm?
Key Takeaways
- Prim’s and Kruskal’s algorithms are used to find the minimum weight spanning tree in a weighted graph.
- Both algorithms utilize a greedy approach and provide optimal solutions.
- Prim’s algorithm grows the tree from a starting vertex, while Kruskal’s algorithm selects edges independently.
- Time and space complexity vary between the two algorithms and depend on the number of vertices and edges in the graph.
- Prim’s algorithm is advantageous for finding multiple minimum spanning trees and handling disconnected graphs, while Kruskal’s algorithm provides a non-redundant solution for sparse graphs.
What is Prim’s Algorithm?
Prim’s Algorithm is a graph theory algorithm used to find the minimum-weight spanning tree of a weighted graph. This algorithm is commonly used in various real-world scenarios, including network design, clustering, and route optimization.
The algorithm works by selecting an arbitrary starting vertex and adding the shortest edge that connects that vertex to any other vertex in the graph. Then, the process repeats, considering the newly added vertex as the starting vertex and adding the shortest edge that connects it to any other unvisited vertex.
Prim’s Algorithm is a greedy algorithm that prioritizes selecting the minimum weight edges at each step. This approach guarantees that the resulting tree is connected and has the minimum possible weight. However, it is important to note that the algorithm’s performance may be sensitive to the starting vertex selected.
The advantages of using Prim’s Algorithm include its ability to handle disconnected graphs and find multiple minimum spanning trees. Additionally, the algorithm provides optimal solutions for large-scale graphs and guarantees optimality. On the other hand, the potential disadvantages of using Prim’s Algorithm include its performance in dense graphs with a large number of edges and its unsuitability for graphs with varying edge weights or those requiring real-time updates.
What is Kruskal’s Algorithm?
Kruskal’s algorithm is a popular graph theory algorithm used to find the minimum weight spanning tree (MST) in a weighted graph. The algorithm was named after its inventor, Joseph Kruskal, and was first published in 1956. Kruskal’s algorithm is based on a greedy approach, where we select the edges with the minimum weight and gradually build the MST.
The main objective of Kruskal’s algorithm is to find a set of edges that connects all the vertices in the graph with the minimum possible weight. It works by starting with the smallest edge, and adding the next smallest edge that doesn’t create a cycle until all vertices are connected.
In Kruskal’s algorithm, we begin by sorting all the edges in the graph in ascending order based on their weight. We then consider each edge in turn, starting with the smallest. If adding an edge creates a cycle, we discard that edge and move on to the next edge. If it doesn’t create a cycle, we add the edge to the MST. We repeat this process until all vertices are connected.
The time complexity of Kruskal’s algorithm is O(E log E), where E is the number of edges in the graph. This makes Kruskal’s algorithm more efficient for sparse graphs, where the number of edges is much less than the number of vertices.
One of the potential disadvantages of Kruskal’s algorithm is its reliance on sorting the edges. This can contribute to its overall computational complexity, particularly in scenarios with a large number of edges. Additionally, Kruskal’s algorithm may not be suitable for graphs with varying edge weights or those requiring real-time updates.
Differences between Prim’s and Kruskal’s Algorithm
While Prim’s and Kruskal’s algorithms share the goal of finding the minimum spanning tree in a graph, they differ in their approach to edge selection, computational complexity, and space requirements.
| Prim’s Algorithm | Kruskal’s Algorithm |
|---|---|
| Prim’s algorithm grows the tree from a single vertex, selecting edges that minimize the weight and maintain connectivity. | Kruskal’s algorithm selects the lightest-weight edges independently, prioritizing connectivity as the edges accumulate. |
| The time complexity of Prim’s algorithm is O(ElogV), making it more efficient than Kruskal’s algorithm in dense graphs with many edges. | Kruskal’s algorithm has a higher time complexity of O(ElogE), making it more practical for sparse graphs with fewer edges. |
| Prim’s algorithm requires more memory to maintain the priority queue containing the vertices and their distances. | Kruskal’s algorithm needs more memory to store the edges and sort them by weight. |
These differences in approach and efficiency make Prim’s and Kruskal’s algorithms better suited for particular scenarios. For instance, Prim’s algorithm is more efficient in graphs with a high edge-weight density, while Kruskal’s algorithm performs better in graphs with a low edge-weight density.
Differences between Prim’s and Kruskal’s Algorithm
Prim’s and Kruskal’s algorithms have distinct approaches to solving the minimum spanning tree problem. While both utilize the greedy algorithm approach, they differ in their methods of selecting edges and their computational and space requirements. The primary differences are:
| Prim’s Algorithm | Kruskal’s Algorithm | |
|---|---|---|
| Edge Selection | Prim’s algorithm selects edges based on the weight of the edge and its adjacency to the growing tree, starting from a single vertex and expanding until the minimum weight spanning tree is formed. | Kruskal’s algorithm selects edges based on their weight, regardless of adjacency to the growing tree, adding them to the set of edges until the minimum weight spanning tree is formed. |
| Computational Complexity | The worst-case time complexity of Prim’s algorithm is O(E log V), where E is the number of edges and V is the number of vertices in the graph. | The worst-case time complexity of Kruskal’s algorithm is O(E log E), where E is the number of edges in the graph. |
| Space Complexity | The space complexity of Prim’s algorithm is O(V), where V is the number of vertices in the graph, as it requires a priority queue and an array to store the set of vertices and their corresponding weights. | The space complexity of Kruskal’s algorithm is O(E), where E is the number of edges in the graph, as it requires a disjoint set data structure to keep track of connected components. |
While both algorithms provide optimal solutions, the choice between them depends on the specific problem requirements. Prim’s algorithm is efficient for dense graphs with many edges and is well-suited for finding the minimum weight spanning tree for graphs with varying edge weights. Meanwhile, Kruskal’s algorithm is more efficient for sparse graphs with many vertices and few edges, and is better suited for finding the minimum weight spanning tree for graphs with uniform edge weights.
Time Complexity of Prim’s and Kruskal’s Algorithms
The efficiency of an algorithm is a critical factor while analyzing its performance. In terms of time complexity, the worst-case scenario of Prim’s and Kruskal’s algorithms depends on the number of vertices and edges in the graph.
Prim’s algorithm has a time complexity of O(V^2) when implemented using an adjacency matrix, where V is the number of vertices in the graph. However, using a priority queue for selecting the minimum-weight edge can reduce the time complexity to O(E log V), where E is the number of edges in the graph.
Kruskal’s algorithm has a time complexity of O(E log E), where E is the number of edges in the graph. Sorting the edges in ascending order by weight is a critical factor in determining the time complexity of Kruskal’s algorithm.
Both algorithms have optimal time complexity for sparse graphs, where the number of edges is less than V^2. Prim’s algorithm performs better than Kruskal’s algorithm in dense graphs with a large number of edges.
In scenarios where the number of edges is proportional to the number of vertices, Kruskal’s algorithm outperforms Prim’s algorithm. This is because Kruskal’s algorithm involves sorting the edges, which can be computationally expensive in graphs with a large number of edges.
Applications of Prim’s Algorithm
Prim’s algorithm has numerous practical applications in various fields and industries. The algorithm’s ability to find the minimum weight spanning tree in a weighted graph makes it useful in solving problems related to connectivity and network design.
Here are some specific examples of how Prim’s algorithm is commonly applied:
- Network Design: Prim’s algorithm is used to design efficient network topologies by connecting nodes with the least amount of cable. It helps minimize the cost and complexity of network infrastructure.
- Clustering: Prim’s algorithm can be applied to cluster similar data points in various domains, such as image processing or natural language processing. It helps to group similar data points and simplify complex data sets.
- Map Routing: Prim’s algorithm can be used in mapping applications to find the shortest path between two points on a map. It helps to determine the most efficient route, taking into account the distance and other relevant factors.
Prim’s algorithm can also be used to solve other optimization problems in transportation, logistics, and supply chain management.
Applications of Prim’s Algorithm
Prim’s algorithm is widely used in diverse real-world scenarios, particularly those involving graphs. One of its most common applications is in finding the minimum weight spanning tree of a connected undirected graph. The minimum weight spanning tree helps to identify the most efficient way to connect all the vertices with the least possible weight.
Another practical application of Prim’s algorithm is in network design, where it is used to minimize the total cost of establishing network connections between different points. The algorithm achieves this by selecting the edges with minimum weight, leading to the creation of a connected minimum weight spanning tree.
Clustering is another field that extensively uses Prim’s algorithm. The algorithm helps to identify the most suitable clusters that can be combined to form a cohesive whole. In this case, Prim’s algorithm is used to identify the minimum weight connections between different clusters, leading to an optimal solution.
Applications of Kruskal’s Algorithm
Kruskal’s algorithm plays a crucial role in finding the minimum spanning tree in a graph, particularly in scenarios where the edges need to be selected independently. It is widely used in various real-world applications, including:
- Designing road networks: Kruskal’s algorithm can be used to optimize the design of road networks to select the shortest and most efficient paths between locations.
- Optimizing circuit connections: The algorithm can also be applied to optimize connections between circuits to reduce power consumption and costs.
- Creating scheduling systems: Kruskal’s algorithm can be used to optimize scheduling systems, such as airline schedules or class schedules, to find the most efficient routes or sequences of tasks.
- Clustering: Kruskal’s algorithm can be employed in clustering problems to differentiate similar data objects based on their properties.
Kruskal’s algorithm provides an efficient and optimal solution for finding minimum spanning trees in graph theory problems with edge independence. It also offers a non-redundant solution and is effective for sparse graphs with a large number of vertices and edges.
Advantages of Prim’s Algorithm
Prim’s algorithm has several advantages that make it an efficient and effective solution for finding minimum weight spanning trees in a graph. Some of the main advantages include:
- Guaranteed optimality: Prim’s algorithm guarantees to find the minimum weight spanning tree for a given weighted graph. This means that there is no possibility of finding a better solution using other algorithms.
- Connectivity: Prim’s algorithm prioritizes the minimum weight edges, resulting in a connected minimum weight spanning tree. This feature is particularly useful in network design and clustering.
- Efficient for large-scale graphs: Prim’s algorithm provides efficient solutions for graphs with a large number of edges and vertices. It has a lower time complexity compared to other graph algorithms that can take significantly longer to compute solutions.
- Handles disconnected graphs: Prim’s algorithm can handle disconnected graphs and find multiple minimum spanning trees in such scenarios.
Overall, Prim’s algorithm is an excellent choice for solving minimum spanning tree problems that require optimality, connectivity, and efficiency.
Advantages of Kruskal’s Algorithm
Kruskal’s Algorithm offers several advantages when finding the minimum weight spanning tree of a graph.
- Edge Independence: Kruskal’s Algorithm selects edges independently, allowing for a non-redundant solution to the minimum spanning tree problem.
- Efficiency for Sparse Graphs: Kruskal’s Algorithm is efficient for graphs with a large number of vertices and edges but with relatively few connections.
- Disconnected Graphs: Kruskal’s Algorithm can handle disconnected graphs and still provide a minimum spanning tree solution.
These advantages make Kruskal’s Algorithm a suitable choice for scenarios that require a non-redundant, efficient, and effective solution for the minimum spanning tree problem. For instance, Kruskal’s Algorithm has been used to design road networks and optimize circuit connections.
Disadvantages of Prim’s Algorithm
While Prim’s algorithm has several advantages, it also has potential disadvantages that users should consider:
- Sensitivity to Starting Vertex: Prim’s algorithm is highly sensitive to the choice of the starting vertex. The algorithm’s efficiency may vary significantly depending on the vertex selected, leading to suboptimal solutions.
- Performance in Dense Graphs: Prim’s algorithm may not perform as efficiently in dense graphs with a large number of edges. The algorithm’s time complexity may increase significantly, slowing down the solution’s calculation process.
- Not Suitable for Real-Time Updates: Prim’s algorithm may not be ideal for graphs that require real-time updates or changes. The algorithm requires a complete graph at the beginning of the solution process, making it impractical for graphs that frequently change.
- May Not Accommodate Varying Edge Weights: Prim’s algorithm assumes that all edges in the graph have the same weight. Therefore, it may not be suitable for graphs with varying edge weights, such as those that change over time.
“Prim’s algorithm is highly sensitive to the choice of the starting vertex.”
Users should consider these potential disadvantages of Prim’s algorithm when selecting which Minimum Spanning Tree algorithm to use.
Dissadvantages of Kruskal’s Algorithm
Kruskal’s algorithm has some potential disadvantages that should be taken into account when selecting an algorithm for solving graph problems. One of the main drawbacks is its time complexity, particularly when dealing with large graphs with many edges. Sorting the edges can be time-consuming, making Kruskal’s algorithm less efficient in these cases.
Another drawback is that Kruskal’s algorithm may not be suitable for graphs with varying edge weights, as it is intended for finding a minimum weight spanning tree. The algorithm may not provide the optimal solution in these cases.
In addition, Kruskal’s algorithm requires more space than Prim’s algorithm, as it needs to store a list of edges and check for cycles. This can be a concern when working with graphs with many vertices and edges or when operating in a memory-constrained environment.
“Kruskal’s algorithm can be time-consuming when dealing with large graphs with many edges.”
Overall, Kruskal’s algorithm is a reliable and widely used graph algorithm. However, it is important to keep its potential drawbacks in mind and compare it with other algorithms, such as Prim’s algorithm, to choose the most suitable one for a given situation.
Conclusion
In conclusion, the differences between Prim’s and Kruskal’s algorithms lie in their approaches to edge selection, computational complexity, and space requirements. Despite these differences, both algorithms utilize a greedy approach and provide optimal solutions for finding minimum spanning trees. The time and space complexity of each algorithm also depend on the number of vertices and edges in the graph.
Prim’s algorithm focuses on growing a tree from a single vertex, while Kruskal’s algorithm selects edges independently. Practical applications of Prim’s algorithm include network design and clustering, while Kruskal’s algorithm is commonly applied in designing road networks and optimizing circuit connections.
One of the advantages of Prim’s algorithm is its ability to handle disconnected graphs and find multiple minimum spanning trees while Kruskal’s algorithm provides a non-redundant solution. Both algorithms guarantee optimality and efficiency, but Prim’s algorithm may not be suitable for dense graphs with a large number of edges, while Kruskal’s algorithm may not perform well in scenarios with varying edge weights or real-time updates.
Overall, the choice between Prim’s and Kruskal’s algorithms depends on the specific graph and problem at hand. When selecting a graph algorithm, it is crucial to consider factors such as time and space complexity. Both Prim’s and Kruskal’s algorithms play a significant role in finding minimum spanning trees and have widespread applications in various fields, including network design, circuit connections, and clustering.
FAQ
Q: What is the difference between Prim’s and Kruskal’s Algorithm?
A: Prim’s and Kruskal’s algorithms are both used to find the minimum spanning tree in a graph, but they differ in their approaches to edge selection, computational complexity, and space requirements.
Q: What is Prim’s Algorithm?
A: Prim’s algorithm is a graph algorithm used to find the minimum-weight spanning tree in a weighted graph. It works by selecting and growing the tree from a starting vertex in a step-by-step process. Prim’s algorithm utilizes the greedy algorithm approach and has advantages and disadvantages in its application.
Q: What is Kruskal’s Algorithm?
A: Kruskal’s algorithm is a graph algorithm used to find the minimum-weight spanning tree in a weighted graph. It works by selecting and adding edges based on their weight, independently of each other. Kruskal’s algorithm also utilizes the greedy algorithm approach and has its own advantages and disadvantages.
Q: What are the similarities between Prim’s and Kruskal’s Algorithm?
A: Prim’s and Kruskal’s algorithms share the goal of finding the minimum spanning tree in a graph and both use a greedy strategy to provide optimal solutions. These algorithms are widely applied in various real-world scenarios.
Q: What are the differences between Prim’s and Kruskal’s Algorithm?
A: Prim’s algorithm focuses on growing a tree from a single vertex, while Kruskal’s algorithm selects edges independently. Additionally, Prim’s algorithm has different computational complexity and space requirements compared to Kruskal’s algorithm.
Q: What is the time complexity of Prim’s and Kruskal’s Algorithms?
A: The time complexity of Prim’s and Kruskal’s algorithms depends on the number of vertices and edges in the graph. Both algorithms have different worst-case time complexities, and their performance may vary depending on the specific scenario.
Q: What is the space complexity of Prim’s and Kruskal’s Algorithms?
A: The space complexity of Prim’s and Kruskal’s algorithms is determined by factors such as the number of vertices and edges in the graph. Each algorithm has its own memory requirements, and the choice between them may depend on the available resources and specific needs.
Q: What are the applications of Prim’s Algorithm?
A: Prim’s algorithm is commonly applied in solving problems related to connectivity and finding the minimum weight spanning tree in a graph. It has practical uses in network design, clustering, and other scenarios where minimum spanning trees are required.
Q: What are the applications of Kruskal’s Algorithm?
A: Kruskal’s algorithm is often utilized in finding the minimum weight spanning tree in a graph, considering edges independently. It is commonly applied in designing road networks, optimizing circuit connections, and other situations where minimum spanning trees are needed.
Q: What are the advantages of Prim’s Algorithm?
A: Prim’s algorithm prioritizes the minimum weight edges, resulting in a connected minimum weight spanning tree. It guarantees optimality and provides efficient solutions for large-scale graphs. It can also handle disconnected graphs and find multiple minimum spanning trees.
Q: What are the advantages of Kruskal’s Algorithm?
A: Kruskal’s algorithm selects edges independently and creates a minimum weight spanning tree. It handles disconnected graphs and provides a non-redundant solution. It is efficient for sparse graphs with a large number of vertices and edges.
Q: What are the disadvantages of Prim’s Algorithm?
A: Prim’s algorithm is sensitive to the choice of the starting vertex and may not perform well in dense graphs with a large number of edges. It may not be suitable for graphs with varying edge weights or those requiring real-time updates.
Q: What are the disadvantages of Kruskal’s Algorithm?
A: Kruskal’s algorithm has a time complexity that can be problematic in scenarios with a large number of edges. It relies on sorting the edges, which contributes to its overall computational complexity. It may also not be suitable for graphs with varying edge weights or those requiring real-time updates.